3.17 - 3.18 Undecidability and Algorithmic Efficiency Notes and Hacks
Markdown post of the group lesson for 3.17-3.18
- Notes
- Hacks
- Combine Hailstone and Number of Iterations
- Write one algorithm that is efficient and one that is inefficient. Compare them and explain why one is and why one isn’t efficient.
- How one algorithm can be more efficient than annother using mathematical and formal reasoning
- Use variables, if statements, and loops to program an algorithm
Notes
Unsolvable vs undecidable
- Unsolvable: is that no algorithm can be written to get the answer to it
- Undecidable: There is no code that can find the answer, because it is too complext, but there is an answer.
Undecidability Example
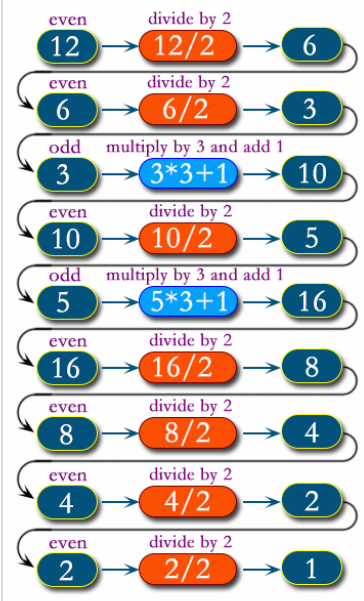
- We do not know if there is a number that will solve this pattern.
- There is an infinite amount of inputs, and we don’t know which one will run the code infinitely.
Vocab
Collatz Conjecture
- one of the most famous unsolved problems in mathematics.
- it asks whether repeating two simple arithmetic operations will eventually transform every positive integer into 1.
Hailstone numbers
- The sequence of integers generated by Collatz conjecture
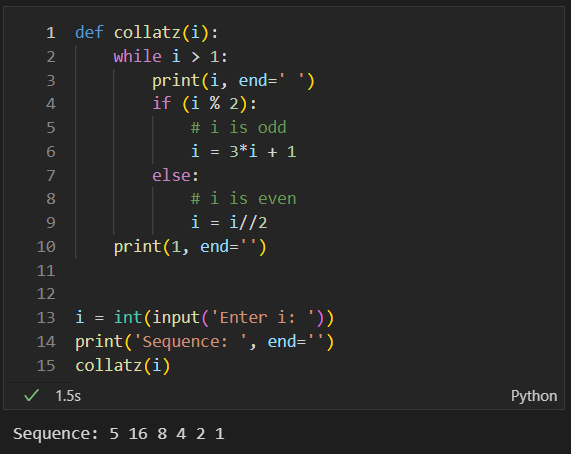
- Examples: Input : N = 7 Output : Hailstone Numbers: 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1 No.
- Code terminates at 1.
Undecidable problems
- A Problem that should give a “yes” or “no” answer, but yet no algorithm exists that can answer correctly on all inputs.
Iteration
- The action or a process of iterating or repeating:
- such as. : a procedure in which repetition of a sequence of operations yields results successively closer to a desired result.
Hailstone Numbers Code Example
Algorithm Efficiency
- Inefficient algorthims are slower and could sometimes take more processing and computing power to run
Hacks
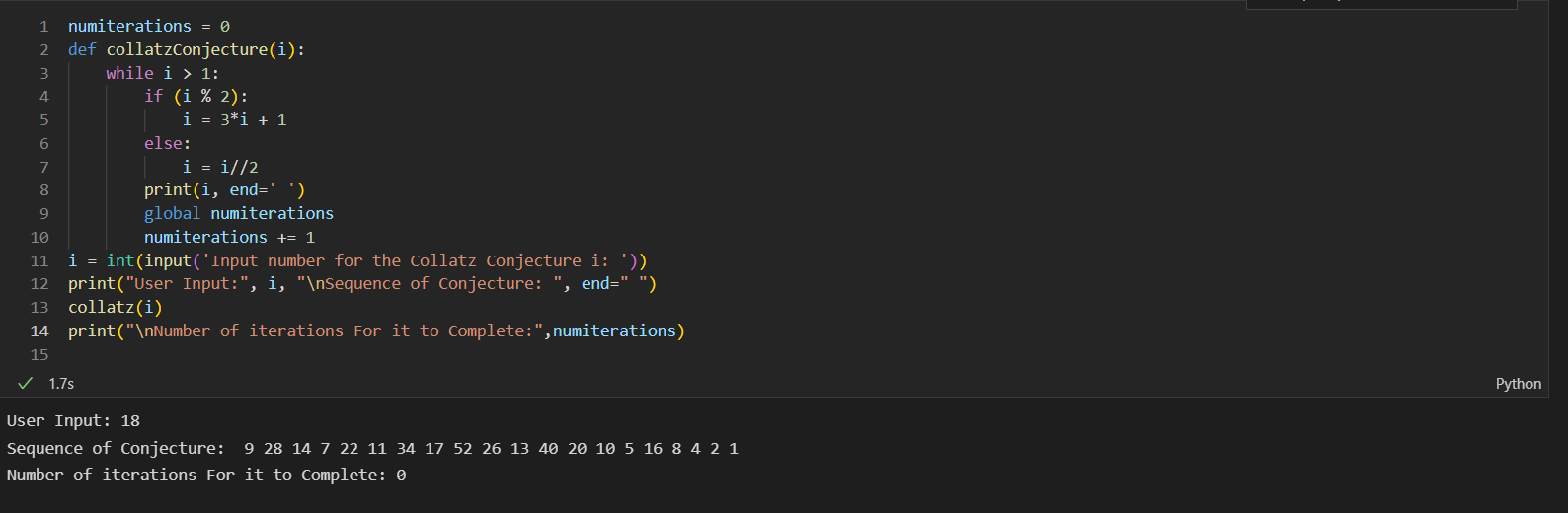
Combine Hailstone and Number of Iterations
- Here is an efficient code for the Collatz conjecture that combined the number of iteraions and the Hailstone numbers:
Write one algorithm that is efficient and one that is inefficient. Compare them and explain why one is and why one isn’t efficient.
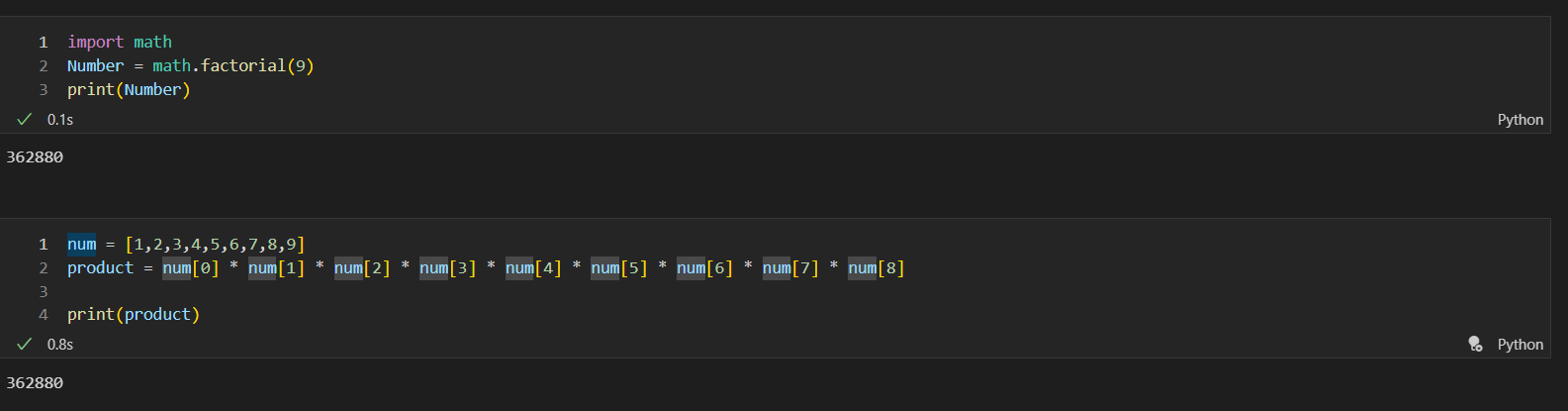
- As you can see, I have coded 2 algorithms that find the factorial of 8.
- The first one is clearly way more efficient since I used the import math library and used the factorial function to find the factorial of 8. On the other hand, the second one manually multiplies 8765432*1 which is clearly way less efficient and more clunky
- The first algorithm is not only easier to read and faster to code, it runs much faster (only 0.1 secs) while the less efficient algorithm took 8 times longer (.8 seconds) to run.
- Furthermore the first algorithm is certainly less efficent than the first because of its easier readability and faster runtime.
How one algorithm can be more efficient than annother using mathematical and formal reasoning
- There are several factors that can contribute to the efficiency of an algorithm. One of the main factors is the time complexity of the algorithm, which is a measure of how long the algorithm takes to run as a function of the size of the input.
- An algorithm with a lower time complexity will generally be more efficient than an algorithm with a higher time complexity, because it will take less time to complete for large inputs.
- The amount of memory that the running of an algorithm uses up is another factor in determining the efficiency of it. Algorithms that use more processing and memory power to run are generally less efficient, especially if there is another algorithm that uses less memory and processing power to achieve the same task.
Use variables, if statements, and loops to program an algorithm
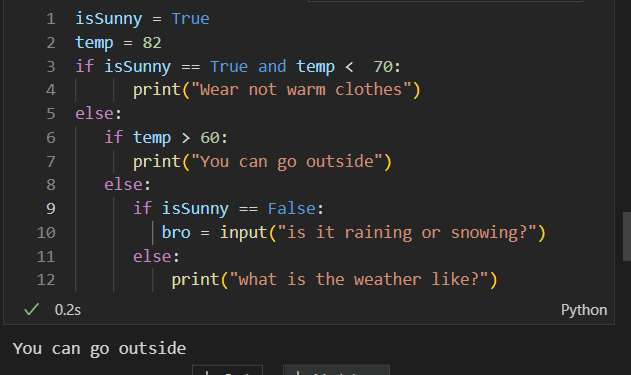
- This algorithm that I coded tells you whether you should go outside or not based on the inputted temperature outside.