3.9 and 3.11 Algorithms Notes and Hacks
Markdown post of the group lesson for 3.9 and 3.11
- Notes
- Hacks
- Algorithms
- Make an algorithm with natural language, a flow chart, and code. Should use Selection or iteration.
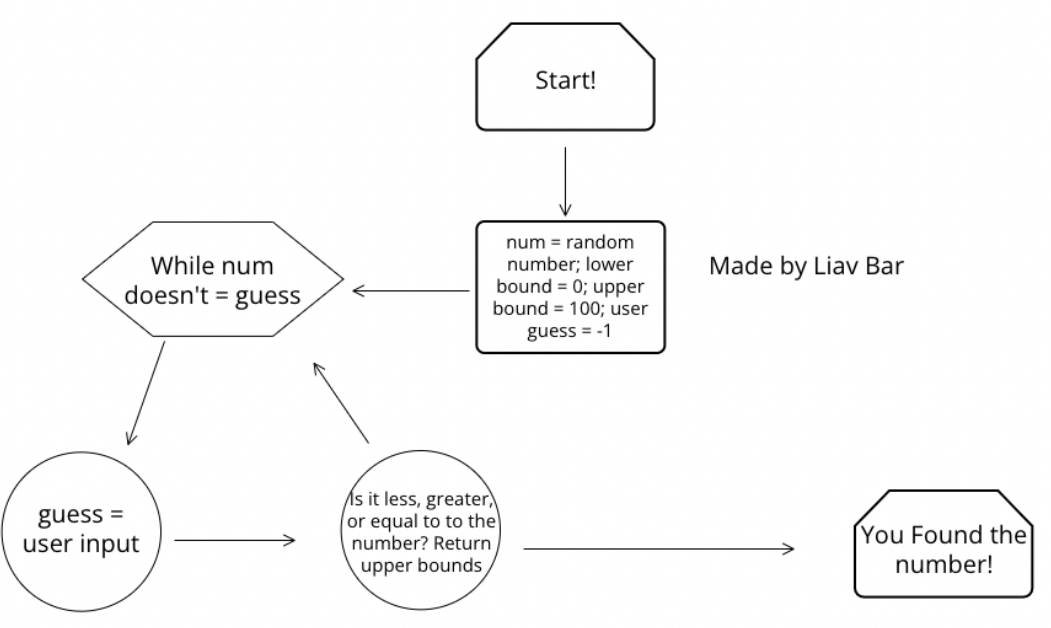
- Fix number guessing game and give more encouraging feedback, make flow chart
- Calculate middle index and create binary tree, what is the second number? which of the lists cannot be a be a binary search be used to find a targetted value.
Notes
Algorithms Review
- Three components of an algorithm are:
- Selection
- Sequence
- Iteration
- Different algorithms can be used to achieve the same result
- Algorithms that look the same can also have different results
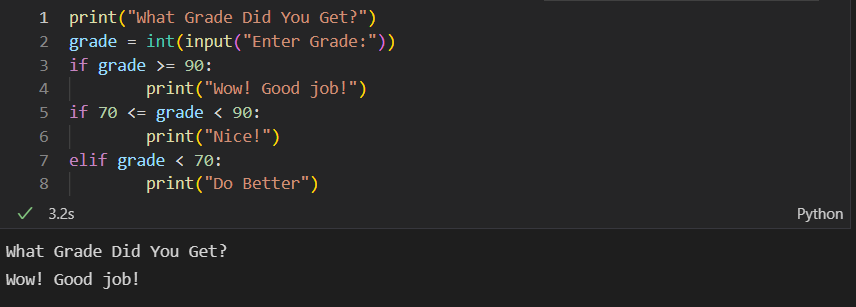
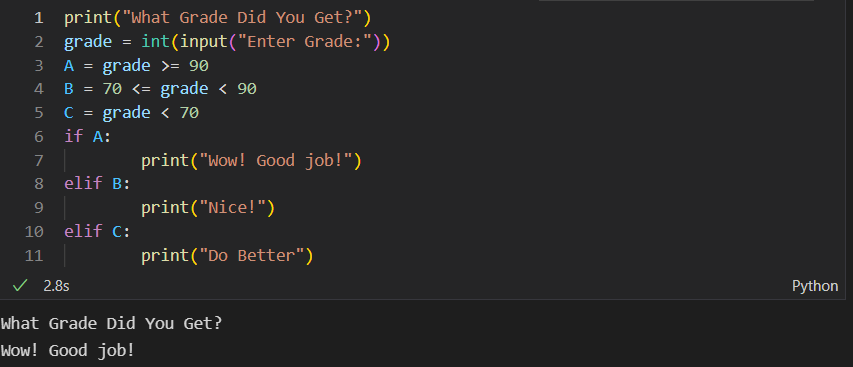
-
As you can see these are slightly different codes, but since I inputed the same grade (93 NOT 90 lol) for both, I recivied the same result.
-
Its kind of like debugging how very small changes in similar algorithms can make durastic differences.
-
Can help display to future self or other people what each part of the code does.
Nested Conditional statements
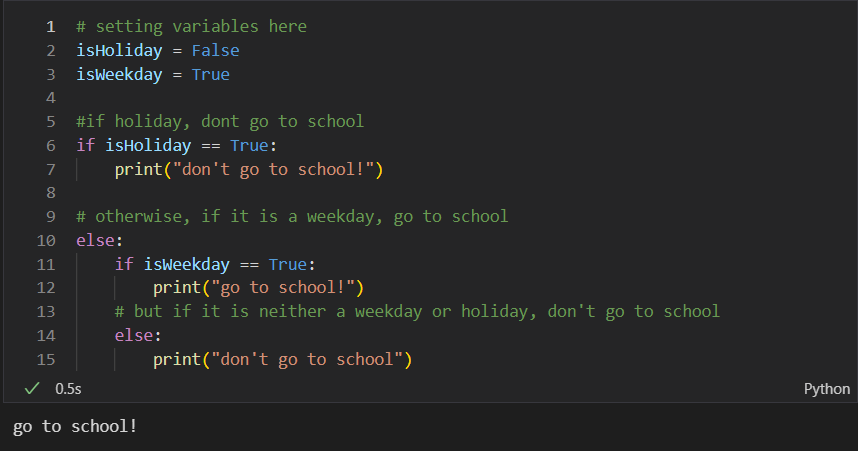
- This nested conditional displays an algorithm that tells you whether you should go to school or not depending on the day of the week.
Developing Algorithms
- Outline the process of the code first so you ensure that it is sequenced correctly
- Its good to make a flowchart to visualize all the steps of the process
- Makes the coding process more effective.
- Start off with doing it in natural lingo, rather than a flow chart.
- Algorithms with iteration repeat a function until a goal is reached
- To more easily represent an algorithm without showing all the repeated steps, we can use iteration
- Algorithms with selection only go through certain functions if certain things are true or false
Example
The parking rate for a garage is as follows:
Less than one hour: Free
1-2 hours: $5
2-3 hours: $8
3-4 hours: $10
4+ hours: $12
- Start
- Input number of hours parked
- If hours is less than 1, cost is free
- If hours is between 1 and 2, cost is $5
- If hours is between 2 and 3, cost is $8
- If hours is between 3 and 4, cost is $10
- If hours is more than 4, cost is $12
- Display cost and goodbye
- Finish

- I inputted “4 hours parked” and the algorithm determined that my parking would cost $12.
Using preexisting algorithms
- Knowing existing algorithms can help construct new ones
- simple existing algorithms can include
- determining min or max of two or more numbers
- computing the sum or average
- identifying if an integer is even or odd
- Using existing correct algorithms can help as building blocks to reduce development time, testing, and identification of errors
- You don’t need to code everything from the ground up.
- Modifying the preexisting code, you can develop on it and make a better code.
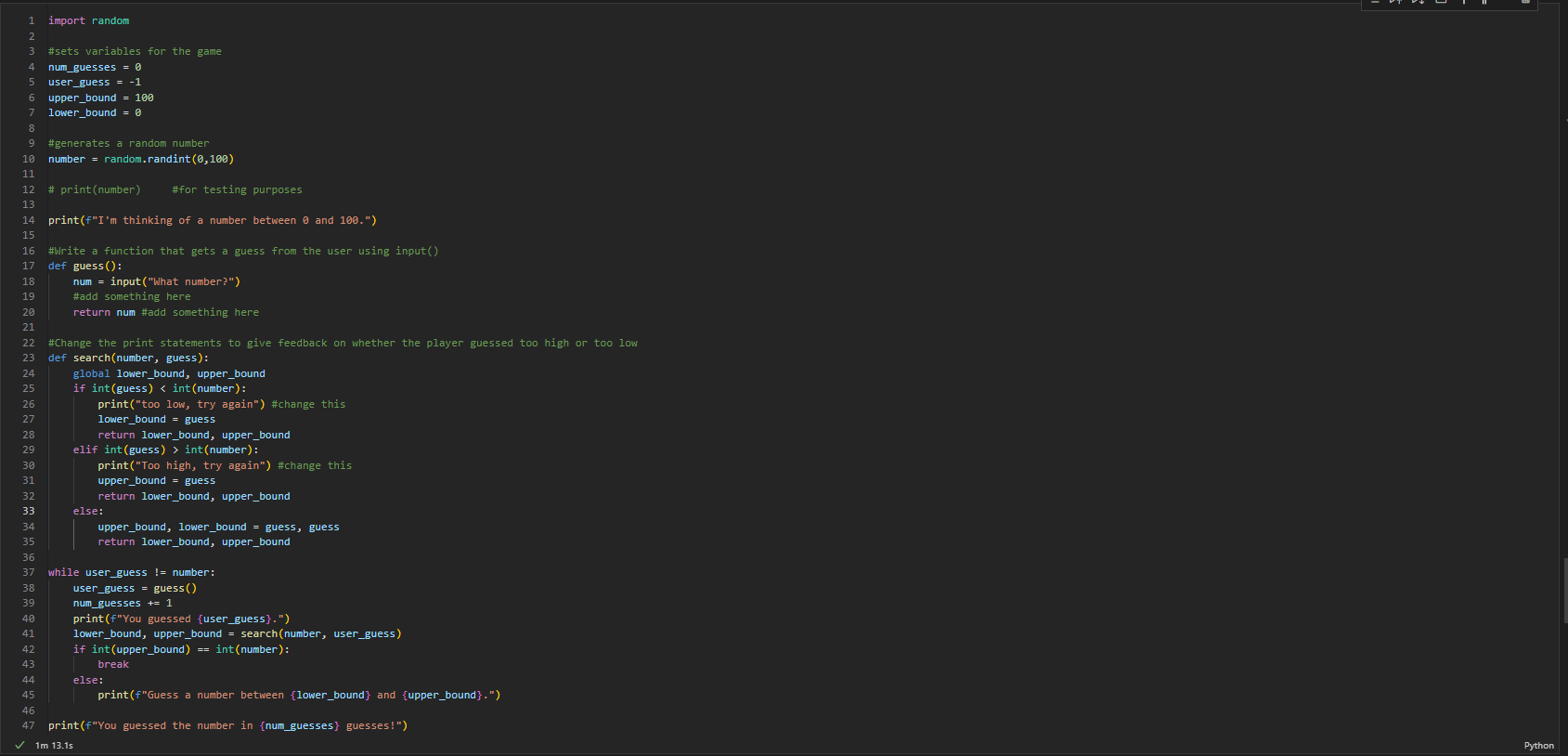
Binary Search
Steps:
- first put the numbers in order
- ascending
- descending
- find the middle number first
- this is found by taking the highest index number plus the lowest index number and divide by 2
- the numbers on the right will be greater and the numbers on the left will be smaller
- this can be represented with a binary tree
- middle number with the smaller number branched off on the left and bigger numbers branched off on the right
- these lists are not always numbers
- lists can be made with strings
- ex. [“apple”, “banana”, “cherry”, “peach”, “watermelon”]
- alphabetical order
- a-z
Hacks
Algorithms
- why is it important to know that algorithms that look different can do the same thing and that algorithms that look the same might have different results?(0.15)
- It is important to understand that similar algorithms have different results, because it is good to know that there are different ways to accomplish the same task.
- Programs can also have similar looking codes but have different outputs. This is important to know when you troubleshoot code to find out what is wrong.
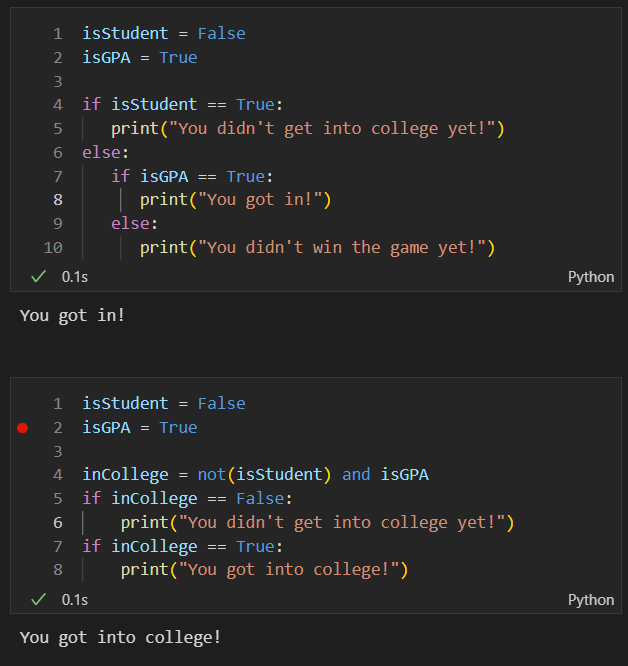
- As you can see these codes that I made are extremely similar and serve a very similar purpose, but they have slight differences.
Make an algorithm with natural language, a flow chart, and code. Should use Selection or iteration.
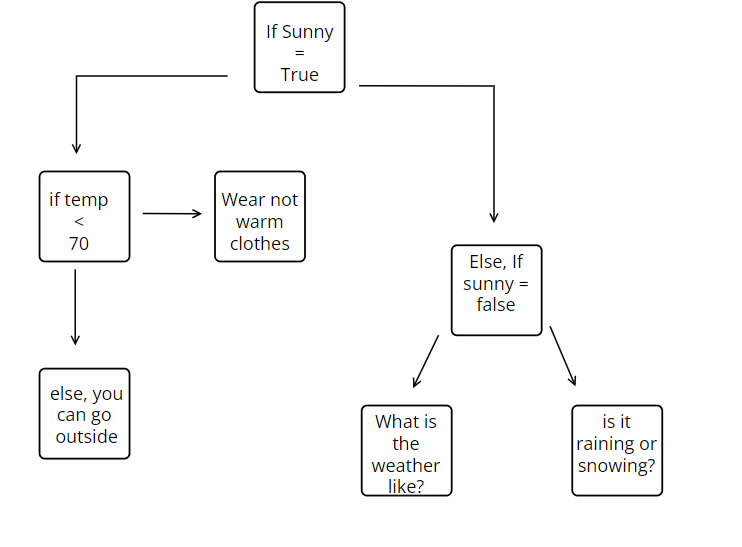
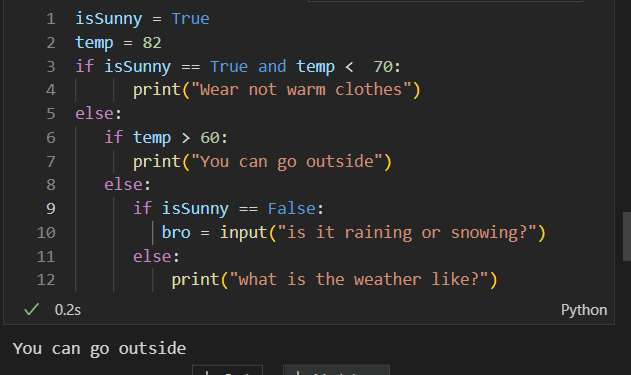
Natural Language:
- It is Sunny
- If it is below 70 degrees wear not warm clothes
- Else, you can go outside
- If it is not false ask if it is raining or snowing
Flow Chart
Code
Fix number guessing game and give more encouraging feedback, make flow chart
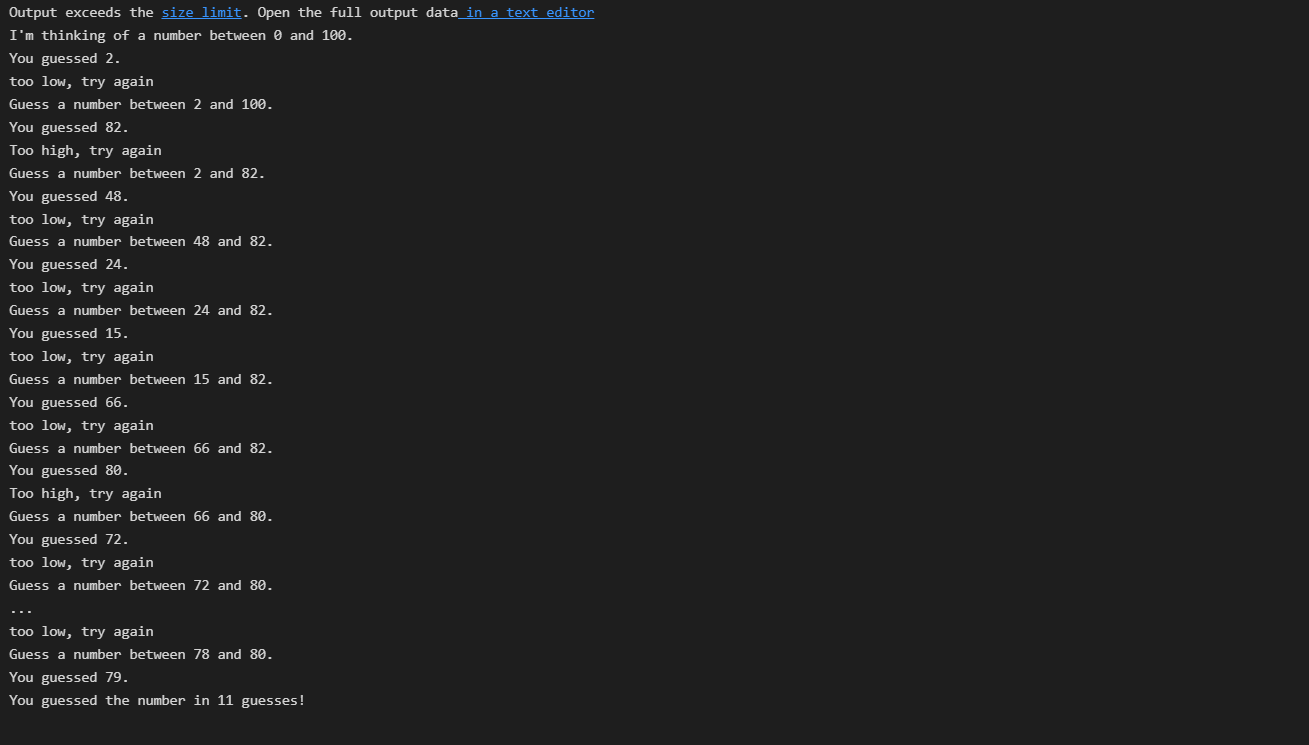
Calculate middle index and create binary tree, what is the second number? which of the lists cannot be a be a binary search be used to find a targetted value.
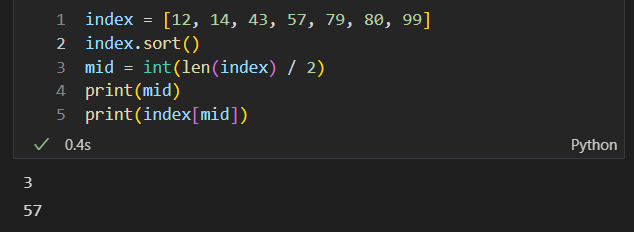
Set 1
- Middle index:
- Flow Chart

- The second number looked at in a binary search would be 80
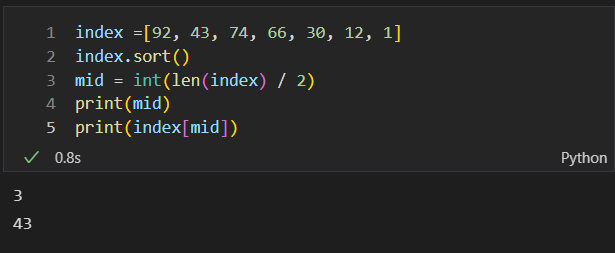
Set 2
- Middle Index:
- Flow Chart
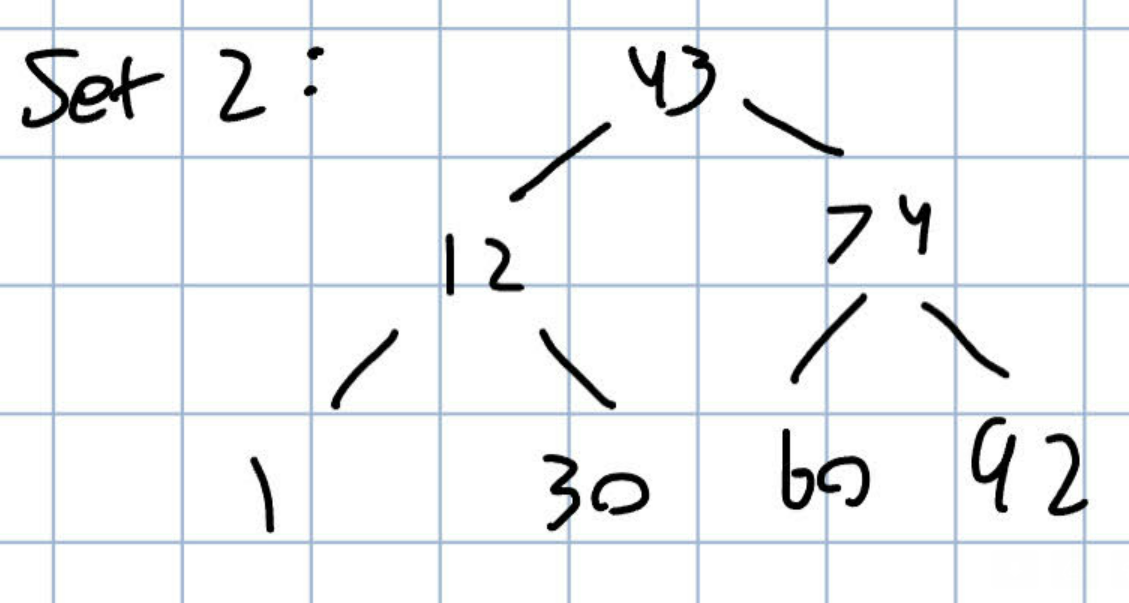
- The second number looked at in a binary search would be 74
Set 3
- Middle Index
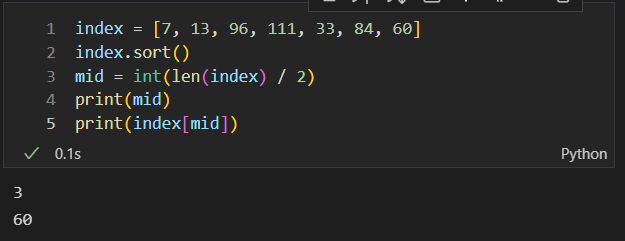
- Flow Chart
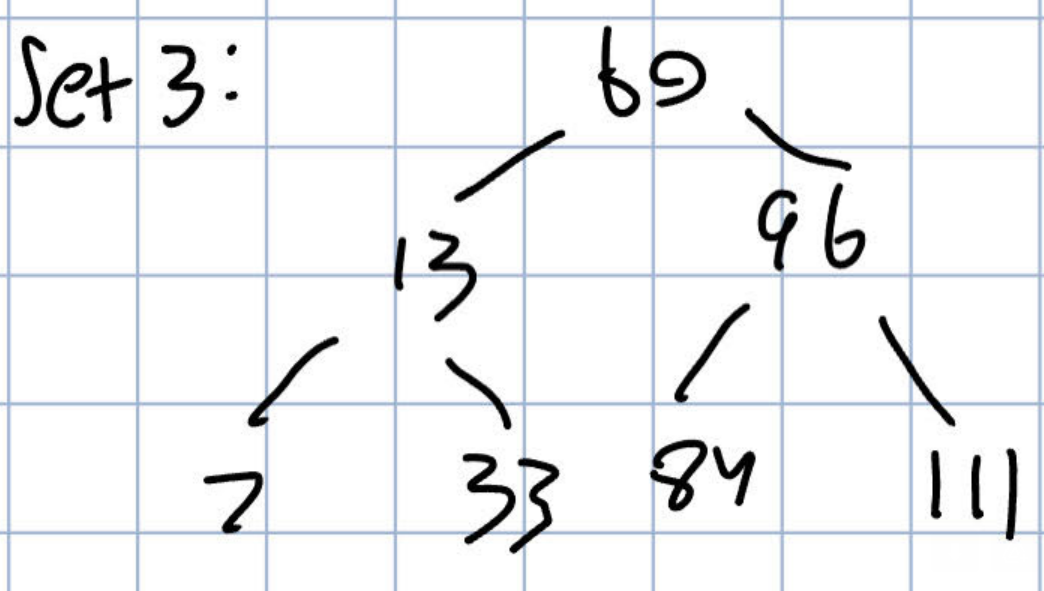
- The second number looked at in a binary search would be 96
- The list that can not use a binary search to find a targeted value is C. [3, 2, 8, 12, 99] because it is unsorted.